Similar Triangles - Sample Problems.doc 4d5q2r

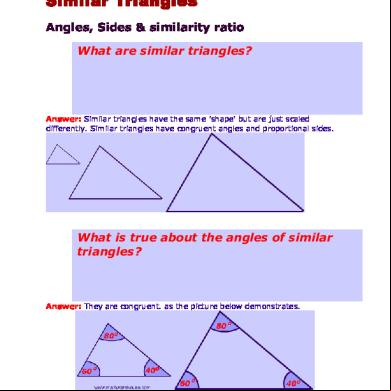
Similar Triangles Angles, Sides & similarity ratio What are similar triangles?

Answer: Similar triangles have the same 'shape' but are just scaled differently. Similar triangles have congruent angles and proportional sides.

What is true about the angles of similar triangles?

Answer: They are congruent. as the picture below demonstrates.

What is true about the sides of similar triangles?

Answer: Corresponding sides of similar triangles are proportional. The example below shows two triangle's with their proportional sides ..

What is the similarity ratio (aka scale factor)?

Answer: It's the ratio between corresponding sides. In the picture above, the larger triangle's sides are two times the smaller triangles sides so the scale factor is 2

16⋅2 = 32 22⋅2 = 44

25⋅2 = 50 Notation: △ABC~△XYZ means that "△ABC is similar to △XYZ"

How do you find the similarity ratio?

Answer: Match up any pair of corresponding sides and set up a ratio. That's it! Example If

△ABC~△WXY, then what is the similarity ratio?

Step 1) Pick a pair of corresponding sides (follow the letters )

AB and WX are corresponding. Follow the letters: △ABC ~ △WXY

Step 2) Substitute side lengths into proportion

ABWX=721

Step 3) Simplify (if necessary)

721=13

Why is the following problem unsolvable?

If △ JKL ~ ratio?

△ XYZ, LJ = 22 ,JK = 20 and YZ = 30, what is the similarity

Answer: You are not given a single pair of corresponding sides so you cannot find the similarity ratio. How to Find corresponding sides Corresponding sides follow the same letter order as the triangle name so YZ of

△XYZ corresponds with side KL of△JKL

JK of

△JKL corresponds with side XY of△XYZ

LJ of

△JKL corresponds with side ZX of△XYZ

Below is a picture of what these two triangles could look like

Practice Problems Problem 1 If ratio?

△ ABC ~ △ADE , AB = 20 and AD = 30, what is the similarity

Step 1) Pick a pair of corresponding sides (follow the letters )

AB and AD are corresponding based on the letters of the triangle names △ABC ~ △ADE

Step 2) Substitute side lengths into proportion

ABAD=2030

Step 3) Simplify (if necessary)

2030=23

Part B) If EA = 33, how long is CA? EA and CA are corresponding sides ( △ABC ~ △ADE) Since the sides of similar triangles are proportional, just set up a proportion involving these two sides and the similarity ratio and solve.

EACA=3233CA=32CA⋅3=2⋅33CA⋅3=66CA=663=22 DE = 27, how long is BC? EA and AC are corresponding sides ( △ABC ~ △ADE) Since the sides of similar triangles are proportional, just set up a proportion involving these two sides and the similarity ratio and solve.

DEBC=3227CA=32CA⋅3=2⋅27CA⋅3=54CA=543=18 Problem 3) Use your knowledge of similar triangles to find the side lengths below.

Step 1) Pick a pair of corresponding sides (follow the letters )

Step 2) Substitute side lengths into

HY and HI are corresponding sides △HYZ ~ △HIY

HYHI=812

(You could, of course, have flipped this fractionif you

wanted to put HI in the numerator HIHY )

proportion

Step 3) Simplify (if necessary)

812=23

Step 4) Set up equation involving ratio and a pair of corresponding sides

23=YZIJ23=YZ92⋅93=YZYZ=6

Finding ZJ is a bit more tricky . You could use the side splitter short cut . Or you use the steps up above to find the length of HJ ,which is 6 and then subtract HZ (or 4) from that to get the answer.

Problem 4) Below are two different versions of △ HYZ and △ HIJ . The only difference between the version is how long the sides are. Only one of these two versions includes a pair of similar triangles. Can you identify which version represents similar triangles?

Similar Triangles Two triangles are Similar if the only difference is size (and possibly the need to turn or flip one around). These triangles are all similar:

(Equal angles have been marked with the same number of arcs) Some of them have different sizes and some of them have been turned or flipped. Similar triangles have: • •

all their angles equal corresponding sides have the same ratio

Corresponding Sides In similar triangles, the sides facing the equal angles are always in the same ratio. For example:

Triangles R and S are similar. The equal angles are marked with the same numbers of arcs. What are the corresponding lengths? • •

The lengths 7 and a are corresponding (they face the angle marked with one arc) The lengths 8 and 6.4 are corresponding (they face the angle marked with two arcs)

•

The lengths 6 and b are corresponding (they face the angle marked with three arcs)

Calculating the Lengths of Corresponding Sides It may be possible to calculate lengths we don't know yet. We need to: • •

Step 1: Find the ratio of corresponding sides in pairs of similar triangles. Step 2: Use that ratio to find the unknown lengths.

Step 1: We know all the sides in Triangle R, and We know the side 6.4 in Triangle S (the other sides we call "a" and "b"). The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle R. So we can match 6.4 with 8, and so the ratio of sides in triangle S to triangle R is: 6.4 to 8 = 64 : 80 = 4 : 5 Now we know that the lengths of sides in triangle S are all 4/5 times the lengths of sides in triangle R.

Step 2: And we can then work out a and b: • •

a faces the angle with one arc as does the side of length 7 in triangle R. b faces the angle with three arcs as does the side of length 6 in triangle R.

Therefore: • • Done!

a = 4/5 × 7 = 28/5 = 5.6 b = 4/5 × 6 = 24/5 = 4.8

How to tell if triangles are similar Any triangle is defined by six measures (three sides, three angles). But you don't need to know all of them to show that two triangles are similar. Various groups of three will do. Triangles are similar if: 1. AAA (angle angle angle) All three pairs of corresponding angles are the same. See Similar Triangles AAA. 2. SSS in same proportion (side side side) All three pairs of corresponding sides are in the same proportion See Similar Triangles SSS. 3. SAS (side angle side) Two pairs of sides in the same proportion and the included angle equal. See Similar Triangles SAS.

Similar Triangles can have shared parts Two triangles can be similar, even if they share some elements. In the figure below, the larger triangle PQR is similar to the smaller one STR. S and T are the midpoints of PR and QR respectively. They share the vertex R and part of the sides PR and QR. They are similar on the basis of AAA, since the corresponding angles in each triangle are the same. Try this Drag any orange dot at a vertex of the outer triangle, the inner triangle will change to remain similar to it, with each corresponding side half the length of the other.

How To Find if Triangles are Similar Two triangles are similar if they have: • •

all their angles equal corresponding sides are in the same ratio

But we don't have to know all three sides and all three angles ...two or three out of the six is enough.

There are three ways to find if two triangles are similar: AA, SAS and SSS:

AA AA stands for "angle, angle" and means that the triangles have two of their angles equal. If two triangles have two of their angles equal, the triangles are similar. For example, these two triangles are similar:

If two of their angles are equal, then the third angle must also be equal, because angles of a triangle always add to make 180°. In this case the missing angle is 180° - (72° + 35°) = 83°. So AA could also be called AAA.

SAS SAS stands for "side, angle, side" and means that we have two triangles where: • •

the ratio between two sides is the same as the ratio between another two sides and we we also know the included angles are equal.

If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. For example:

In this example we can see that: • •

one pair of sides is in the ratio of 21 : 14 = 3 : 2 another pair of sides is in the ratio of 15 : 10 = 3 : 2

•

there is a matching angle of 75° in between them

So there is enough information to tell us that the two triangles are similar.

Using Trigonometry We could also use Trigonometry to calculate the other two sides using the Law of Cosines:

In Triangle ABC:

a2 = b2 + c2 - 2bc cos A = 212 + 152 - 2 × 21 × 15 × Cos75° = 441 + 225 - 630 × 0.2588... = 666 - 163.055... = 502.944...

Therefore a = √502.94 = 22.426...

In Triangle XYZ:

x2 = y2 + z2 - 2yz cos X = 142 + 102 - 2 × 14 × 10 × Cos75° = 196 + 100 - 280 × 0.2588... = 296 - 72.469... = 223.530...

Therefore x = √223.530... = 14.950...

Now let us check the ratio of those two sides:

a : x = 22.426... : 14.950... = 3 : 2 the same ratio as before! Note: you could also use the Law of Sines to show that the other two angles are equal.

SSS

SSS stands for "side, side, side" and means that we have two triangles with all three pairs of corresponding sides in the same ratio. If two triangles have three pairs of sides in the same ratio, then the triangles are similar. For example:

In this example, the ratios of sides are: • •

a: x = 6 : 7.5 = 12 : 15 = 4 : 5 b: y = 8 : 10 = 4 : 5

•

c: z = 4 : 5

These ratios are all equal, so the two triangles are similar.

Using Trigonometry Using Trigonometry we can show that the two triangles have equal angles by using the Law of Cosines in each triangle:

In Triangle ABC:

cos A

= (b² + c² - a²)/2bc = (8² + 4² - 6²)/(2× 8 × 4) = (64 + 16 - 36)/64 = 44/64 = 0.6875

Therefore Angle A = 46.6°

In Triangle XYZ:

cos X = = (y² + z² - x²)/2yz = (10² + 5² - 7.5²)/(2× 10 × 5) = (100 + 25 - 56.25)/100 = 68.75/100 = 0.6875

Therefore Angle X = 46.6°

So angles A and X are equal! Similarly you can show that angles B and Y are equal, and angles C and Z are equal.

Congruent If one shape can become another using Turns, Flips and/or Slides, then the two shapes are called Congruent:

Rotation

Turn!

Reflection

Flip!

Translation

Slide!

After any of those transformations (turn, flip or slide), the shape still hasthe same size, area, angles and line lengths.

Examples These shapes are all Congruent:

Rotated

Reflected and Moved

Reflected and Rotated

Congruent or Similar? The two shapes need to be the same size to be congruent. When you need to resize one shape to make it the same as the other, the shapes are called Similar.

If you ...

... only Rotate, Reflect and/or Translate

... also need to Resize

Then the shapes are ...

Congruent

Similar

Congruent? Why such a funny word that basically means "equal"? Probably because they would only be "equal" if laid on top of each other. Anyway it comes from Latincongruere, "to agree". So the shapes "agree"