5.2 Caracteristicas De La Curva Normal y4m4s
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 3l3c15
Overview 3z723u
& View 5.2 Caracteristicas De La Curva Normal as PDF for free.
More details 2i4a6q
- Words: 1,323
- Pages: 13
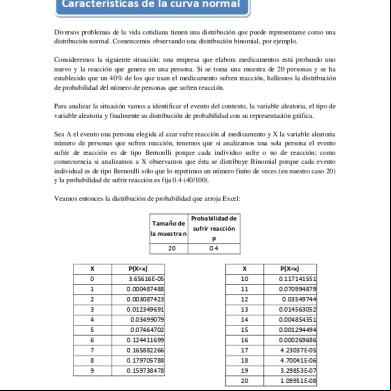
Características de la curva normal Diversos problemas de la vida cotidiana tienen una distribución que puede representarse como una distribución normal. Comencemos observando una distribución binomial, por ejemplo. Consideremos la siguiente situación: una empresa que elabora medicamentos está probando uno nuevo y la reacción que genera en una persona. Si se toma una muestra de 20 personas y se ha establecido que un 40% de los que usan el medicamento sufren reacción, hallemos la distribución de probabilidad del número de personas que sufren reacción. Para analizar la situación vamos a identificar el evento del contexto, la variable aleatoria, el tipo de variable aleatoria y finalmente su distribución de probabilidad con su representación gráfica. Sea A el evento una persona elegida al azar sufre reacción al medicamento y X la variable aleatoria número de personas que sufren reacción, tenemos que si analizamos una sola persona el evento sufrir de reacción es de tipo Bernoulli porque cada individuo sufre o no de reacción; como consecuencia si analizamos a X observamos que ésta se distribuye Binomial porque cada evento individual es de tipo Bernoulli sólo que lo repetimos un número finito de veces (en nuestro caso 20) y la probabilidad de sufrir reacción es fija 0.4 (40/100). Veamos entonces la distribución de probabilidad que arroja Excel: Probabilidad de Tamaño de sufrir reacción la muestra n p 20 0.4 X 0 1 2 3 4 5 6 7 8 9
P(X=x) 3.65616E-05 0.000487488 0.003087423 0.012349691 0.03499079 0.07464702 0.124411699 0.165882266 0.179705788 0.159738478
X 10 11 12 13 14 15 16 17 18 19 20
P(X=x) 0.117141551 0.070994879 0.03549744 0.014563052 0.004854351 0.001294494 0.000269686 4.23037E-05 4.70041E-06 3.29853E-07 1.09951E-08
Distribución de probabilidades Probabilidad
0.2 0.15 0.1 Probabilidad 0.05 0 0 2 4 6 8 10 12 14 16 18 20
Si observamos este mismo gráfico pero no en barras sino en líneas obtenemos la siguiente representación:
Distribución de probabilidades Probabilidad
0.2 0.15 0.1 Probabilidad 0.05 0 0 2 4 6 8 101214161820
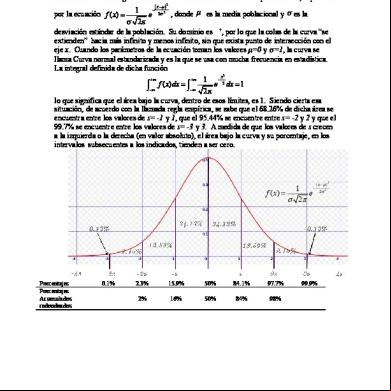
Esta curva es muy similar a la curva de la distribución normal, lo que la diferencia es que la anterior no es simétrica mientras que la distribución normal siempre es simétrica. Sin embargo, entre mayor sea el tamaño de la muestra una distribución binomial puede aproximarse a una distribución normal. Ahora que observamos la similitud de las distribuciones binomial podemos enfocarnos al estudio y análisis de una distribución normal. Características de una curva normal: 1. Tiene forma de campana.
2. Tiene media y varianza 2 .
Media
3. Es una curva simétrica respecto a la media, en otras palabras si nos ubicamos sobre la media lo que observamos a la derecha es exactamente igual a lo que observamos a la izquierda.
4. El valor del área bajo curva es 1 y representa la probabilidad de todo el espacio muestral.
5. Cada probabilidad acumulada que se calcula, con la tabla de la normal, representa el área bajo la curva.
Características de la distribución normal estándar: 1.
Tiene forma de campana.
2. Tiene media y varianza 2 .
Media
3. Es una curva simétrica respecto a la media, en otras palabras si nos ubicamos sobre la media lo que observamos a la derecha es exactamente igual a lo que observamos a la izquierda.
4. El valor del área bajo curva es 1 y representa la probabilidad de todo el espacio muestral. 5. Cada probabilidad acumulada que se calcula, con la tabla de la normal, representa el área bajo la curva.
Uso de la tabla de la distribución normal Como si indicó, las tablas de la distribución normal nos permiten calcular la probabilidad de que una variable aleatoria normal sea inferior o igual a un valor dado. En otras palabras si X es una variable aleatoria normal con media y desviación típica , para calcular P( X x) se debe estandarizar a X para usar la tabla de una distribución normal estándar. Veamos cómo: estandarizamos a X definiendo una nueva variable aleatoria
Z
X
Cuya distribución es normal estándar porque tiene media 0 y varianza 1. Con esto, si queremos calcular P( X x) tan sólo debemos calcular:
x X x P PZ Y buscar el valor de la probabilidad en la tabla de la normal estándar. Debemos tener en cuenta que dicho valor también puede calcularse con Excel. Después de analizar el uso de las tablas veremos cómo usar Excel para dichos cálculos. Existen dos tipos de tablas, una calcula probabilidades como la siguiente:
P( Z z ) Y la otra calcula probabilidades como la siguiente:
P(0 Z z ) En ambos casos la tabla ubica en la columna de la izquierda los valores de z con un decimal y en la primera fila los demás decimales. Por ejemplo, si quisiéramos buscar P( Z 1.49) entonces
z 1.49 y en la columna de la izquierda buscamos a 1.4 y en la primera fila a 0.09; el número que se encuentra ubicado en la fila de 1.4 con la columna 0.09 es el valor de la probabilidad buscada:
El valor sombreado (0.93189) es la probabilidad buscada, esto significa que el área bajo la curva para los valores menores que 1.49 es 0.93189. Por otra parte si nos solicitan P(0 Z 1.49) el valor es 0.43189:
Debemos aclarar que no siempre nos van a solicitar probabilidades como P( Z 1.49) de hecho pueden solicitarnos P( Z 1.49) y para resolverla debemos tener claridad de las propiedades del cálculo de probabilidades. Como en P( Z 1.49) la tabla no nos da dicho valor debemos utilizar la ley del complemento para calcularla: P( Z 1.49) 1 P (Z 1.49) .
De manera similar si nos piden calcular por ejemplo, P(3.01 Z 1.49) necesitamos utilizar la siguiente regla:
P(3.01 Z 1.49) P( Z 1.49) P( Z 3.01) como ambos valores los arroja la tabla sólo debemos buscarlos y realizar la resta correspondiente, nótese que ya tenemos el valor de P( Z 1.49) sólo vamos a buscar P( Z 3.01) :
Así P(3.01 Z 1.49) P( Z 1.49) P( Z 3.01) 0.93189 0.00131 . Esta regla se utiliza tanto para aquellos casos en que ambos valores son negativos, positivos o uno es positivo y el otro negativo.
Cómo usar Excel para calcular probabilidades de la normal Vamos a calcular las probabilidades anteriores con Excel para corroborar que los valores son los mismos. Calculemos: 1.
P( Z 1.49)
En Excel buscamos en la ayuda distribución normal, téngase en cuenta que cada office es distinto según sea 2003, 2007 u otros; en mi caso usaré office 2007.
Escribimos en una casilla de Excel la siguiente fórmula: =distr.norm.estand(z) donde z es el valor que tenemos (en nuestro caso 1.49); damos enter y listo obtenemos el valor buscado.
Si observamos coincide con el valor que nos arrojó la tabla. 2.
P( Z 3.01)
Repetimos el anterior proceso pero ahora con el valor -3.01:
Valor que de nuevo coincide con el de la tabla. Una observación que vale la pena presentar es que puede suceder que se nos pida el proceso contrario, es decir, puede que nos den la probabilidad y nos pidan hallar el número para el cual se tiene dicha probabilidad. Para ello podemos usar las tablas o también Excel.
Averigüemos el valor de z para el cual la probabilidad es de 0.00088; buscamos en la tabla dicho valor y ubicamos el valor de z :
El valor buscado es z 3.13 ; para este valor tenemos P(Z 3.13) 0.00088 . Busquemos el mismo valor con Excel:
Escribimos en una celda =distr.norm.estand.inv(0.00088)
Damos enter y obtenemos el valor -3.1280003 que al redondear nos da -3.13.
P(X=x) 3.65616E-05 0.000487488 0.003087423 0.012349691 0.03499079 0.07464702 0.124411699 0.165882266 0.179705788 0.159738478
X 10 11 12 13 14 15 16 17 18 19 20
P(X=x) 0.117141551 0.070994879 0.03549744 0.014563052 0.004854351 0.001294494 0.000269686 4.23037E-05 4.70041E-06 3.29853E-07 1.09951E-08
Distribución de probabilidades Probabilidad
0.2 0.15 0.1 Probabilidad 0.05 0 0 2 4 6 8 10 12 14 16 18 20
Si observamos este mismo gráfico pero no en barras sino en líneas obtenemos la siguiente representación:
Distribución de probabilidades Probabilidad
0.2 0.15 0.1 Probabilidad 0.05 0 0 2 4 6 8 101214161820
Esta curva es muy similar a la curva de la distribución normal, lo que la diferencia es que la anterior no es simétrica mientras que la distribución normal siempre es simétrica. Sin embargo, entre mayor sea el tamaño de la muestra una distribución binomial puede aproximarse a una distribución normal. Ahora que observamos la similitud de las distribuciones binomial podemos enfocarnos al estudio y análisis de una distribución normal. Características de una curva normal: 1. Tiene forma de campana.
2. Tiene media y varianza 2 .
Media
3. Es una curva simétrica respecto a la media, en otras palabras si nos ubicamos sobre la media lo que observamos a la derecha es exactamente igual a lo que observamos a la izquierda.
4. El valor del área bajo curva es 1 y representa la probabilidad de todo el espacio muestral.
5. Cada probabilidad acumulada que se calcula, con la tabla de la normal, representa el área bajo la curva.
Características de la distribución normal estándar: 1.
Tiene forma de campana.
2. Tiene media y varianza 2 .
Media
3. Es una curva simétrica respecto a la media, en otras palabras si nos ubicamos sobre la media lo que observamos a la derecha es exactamente igual a lo que observamos a la izquierda.
4. El valor del área bajo curva es 1 y representa la probabilidad de todo el espacio muestral. 5. Cada probabilidad acumulada que se calcula, con la tabla de la normal, representa el área bajo la curva.
Uso de la tabla de la distribución normal Como si indicó, las tablas de la distribución normal nos permiten calcular la probabilidad de que una variable aleatoria normal sea inferior o igual a un valor dado. En otras palabras si X es una variable aleatoria normal con media y desviación típica , para calcular P( X x) se debe estandarizar a X para usar la tabla de una distribución normal estándar. Veamos cómo: estandarizamos a X definiendo una nueva variable aleatoria
Z
X
Cuya distribución es normal estándar porque tiene media 0 y varianza 1. Con esto, si queremos calcular P( X x) tan sólo debemos calcular:
x X x P PZ Y buscar el valor de la probabilidad en la tabla de la normal estándar. Debemos tener en cuenta que dicho valor también puede calcularse con Excel. Después de analizar el uso de las tablas veremos cómo usar Excel para dichos cálculos. Existen dos tipos de tablas, una calcula probabilidades como la siguiente:
P( Z z ) Y la otra calcula probabilidades como la siguiente:
P(0 Z z ) En ambos casos la tabla ubica en la columna de la izquierda los valores de z con un decimal y en la primera fila los demás decimales. Por ejemplo, si quisiéramos buscar P( Z 1.49) entonces
z 1.49 y en la columna de la izquierda buscamos a 1.4 y en la primera fila a 0.09; el número que se encuentra ubicado en la fila de 1.4 con la columna 0.09 es el valor de la probabilidad buscada:
El valor sombreado (0.93189) es la probabilidad buscada, esto significa que el área bajo la curva para los valores menores que 1.49 es 0.93189. Por otra parte si nos solicitan P(0 Z 1.49) el valor es 0.43189:
Debemos aclarar que no siempre nos van a solicitar probabilidades como P( Z 1.49) de hecho pueden solicitarnos P( Z 1.49) y para resolverla debemos tener claridad de las propiedades del cálculo de probabilidades. Como en P( Z 1.49) la tabla no nos da dicho valor debemos utilizar la ley del complemento para calcularla: P( Z 1.49) 1 P (Z 1.49) .
De manera similar si nos piden calcular por ejemplo, P(3.01 Z 1.49) necesitamos utilizar la siguiente regla:
P(3.01 Z 1.49) P( Z 1.49) P( Z 3.01) como ambos valores los arroja la tabla sólo debemos buscarlos y realizar la resta correspondiente, nótese que ya tenemos el valor de P( Z 1.49) sólo vamos a buscar P( Z 3.01) :
Así P(3.01 Z 1.49) P( Z 1.49) P( Z 3.01) 0.93189 0.00131 . Esta regla se utiliza tanto para aquellos casos en que ambos valores son negativos, positivos o uno es positivo y el otro negativo.
Cómo usar Excel para calcular probabilidades de la normal Vamos a calcular las probabilidades anteriores con Excel para corroborar que los valores son los mismos. Calculemos: 1.
P( Z 1.49)
En Excel buscamos en la ayuda distribución normal, téngase en cuenta que cada office es distinto según sea 2003, 2007 u otros; en mi caso usaré office 2007.
Escribimos en una casilla de Excel la siguiente fórmula: =distr.norm.estand(z) donde z es el valor que tenemos (en nuestro caso 1.49); damos enter y listo obtenemos el valor buscado.
Si observamos coincide con el valor que nos arrojó la tabla. 2.
P( Z 3.01)
Repetimos el anterior proceso pero ahora con el valor -3.01:
Valor que de nuevo coincide con el de la tabla. Una observación que vale la pena presentar es que puede suceder que se nos pida el proceso contrario, es decir, puede que nos den la probabilidad y nos pidan hallar el número para el cual se tiene dicha probabilidad. Para ello podemos usar las tablas o también Excel.
Averigüemos el valor de z para el cual la probabilidad es de 0.00088; buscamos en la tabla dicho valor y ubicamos el valor de z :
El valor buscado es z 3.13 ; para este valor tenemos P(Z 3.13) 0.00088 . Busquemos el mismo valor con Excel:
Escribimos en una celda =distr.norm.estand.inv(0.00088)
Damos enter y obtenemos el valor -3.1280003 que al redondear nos da -3.13.